REFERENCES
- [1] Lam, K. Y., Liew, K. M. and Chow, S. T., “Use of two-dimensional orthogonal polynomials for vibration analysis of circular and elliptical plates,” Journal of Sound and Vibration, Vol. 154(2), pp. 261�269 (1992).
- [2] Leissa, A. W., “Vibration of plates”, Washington: Office of Technology Utilization. SP-160, NASA (1969).
- [3] Leissa, A. W., “Recent research in plate vibrations: Classical theory,” The Shock and Vibration Digest, Vol. 9(10), pp. 3�24 (1977).
- [4] Leissa, A. W., “Recent research in plate vibrations: Complicating effects,” The Shock and Vibration Digest, Vol. 9(11), pp. 1�35 (1977).
- [5] Leissa, A. W., “Plate vibration research, 1976-1980: Classical theory,” The Shock and Vibration Digest, Vol. 13(9), pp. 11�22 (1981).
- [6] Leissa, A. W., “Plate vibration research: Classical theory,” The Shock and Vibration Digest, Vol. 13(10), pp. 19-36 (1981).
- [7] Leissa, A. W., “Recent studies in plate vibrations: part I, Classical theory,” The Shock and Vibration Digest, Vol. 19(2), pp. 11�18 (1987).
- [8] Leissa, A. W., “Recent studies in plate vibrations: part II, Complicating effects,” The Shock and Vibration Digest, Vol. 19(3), pp. 10�24 (1987).
- [9] Narita, Y., “Free vibration analysis of orthotropic elliptic plates resting on arbitrary distributed point supports,” Journal of Sound and Vibration, Vol. 108(1), pp. 1�10 (1986).
- [10] Rajalingham, C. and Bhat, R. B., “Axisymmetric vibration of circular plates and its analog in elliptical plates using characteristic orthogonal polynomials,” Journal of Sound and Vibration, Vol. 161(1), pp. 109� 118 (1993).
- [11] Rajalingham, C., Bhat, R. B. and Xistris, G. D., “Vibration of clamped elliptic plates using exact circular plates mode as shape function in Rayleigh-Ritz method,” Int. J. of Mech. Sci., Vol. 36, pp. 231�246 (1994).
- [12] Singh, B. and Chakraverty, S., “Transverse vibration of circular and elliptic plates with variable thickness,” Indian. J. of pure. Appl. Math., Vol. 22(9), pp. 787� 803 (1991).
- [13] Singh, B. and Chakraverty, S., “Transverse vibration of completely free elliptic and circular pates using orthogonal polynomials in Rayleigh-Ritz method,” Int. J. Mech. Sci., Vol. 33, pp. 741�751 (1991).
- [14] Singh, B. and Chakraverty, S., “Transverse vibration of circular and elliptic plates with quadratically varying thickness,” Applied Mathematical Model, 16, pp. 269�274 (1992).
- [15] Singh, B. and Chakraverty, S., “Transverse vibration of completely free elliptic and circular plates using orthogonal polynomials in the Rayleigh-Ritz method,” Int. J. Mech. Sci., Vol. 33, pp. 741�751 (1991).
- [16] Singh, B. and Chakraverty, S., “On the use of orthogonal polynomials in the Rayleigh-Ritz method for the study of transverse vibration of elliptic plates,” Computer and Structure, Vol. 43(3), pp. 439�443 (1992).
- [17] Singh, B. and Chakraverty, S., “Transverse vibration of simply supported elliptical and circular plates using boundary characteristic orthogonal polynomials in the two variables,” Journal of Sound and Vibration, Vol. 152(1), pp. 149�156 (1992).
- [18] Singh, B. and Chakraverty, S., “Transverse vibration analysis of annular circular and elliptic plates using the characteristic orthogonal polynomials in two dimensions,” Journal of Sound and Vibration, Vol. 162(3), pp. 537�546 (1993).
- [19] Singh, B. and Chakraverty, S., “Use of characteristic orthogonal polynomials in two dimensions for transverse vibration of elliptic and circular plates with variable thickness,” Journal of Sound and Vibration, Vol. 173(3), pp. 289�299 (1994).
- [20] Chakraverty, S. and Petyt, M., “Natural frequencies for free vibration of non-homogeneous elliptic and circular plates using two dimensional orthogonal polynomials,” Applied Mathematical Modelling, Vol. 21, pp. 53�67, (1997).
- [21] Chakraverty, S. and Petyt, M., “Free vibration analysis of elliptic and circular plates having rectangular orthotropy,” Structural Engineering and Mechanics, Vol. 7, 53�67 (1999).
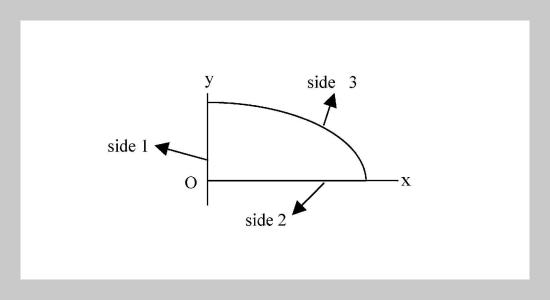
- [22] Singh, B. and Saxena, V., “Transverse vibration of a quarter of an elliptic plate with variable thickness,” Int. J. Mech. Sci., Vol. 37(10), pp. 1103�1132 (1995).
- [23] Singh, B. and Saxena, V., “Transverse vibration of a quarter of a circular plate with variable thickness,” Journal of Sound and Vibration, Vol. 183(1), pp. 49�67 (1995).
- [24] Wang, C. M. and Wang, L., “Vibration and buckling of super elliptic plates,” Journal of Sound and Vibration, Vol. 171, pp. 301�314 (1994).