Wen-Ben Wu This email address is being protected from spambots. You need JavaScript enabled to view it.1, Pang-Chia Chen2 , Gong Chen3 , Koan-Yuh Chang4 and Yeong-Hwa Chang5 1Department of Electrical Engineering, Chin-Min Institute of Technology, Miaoli, Taiwan 351, R.O.C.
2Department of Electrical Engineering, Kao Yuan University, Kaohsiung, Taiwan 821, R.O.C.
3Department of Electrical and Electronic Engineering, National Defense University, Taoyuan, Taiwan 335, R.O.C.
4Department of Electronic Engineering, Chienkuo Technology University, Changhua City, Taiwan 500, R.O.C.
5Department of Electrical Engineering, Chang Gung University, Taoyuan, Taiwan 333, R.O.C.
Received:
September 6, 2007
Accepted:
June 3, 2008
Publication Date:
March 1, 2009
Download Citation:
||https://doi.org/10.6180/jase.2009.12.1.06
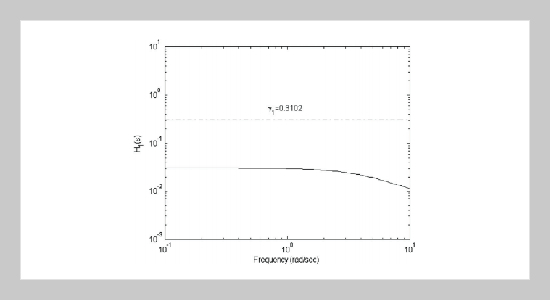
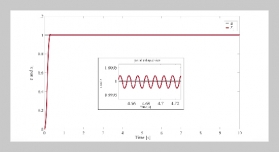
The present paper investigates the problem of robustly decentralized H∝ state feedback controller with state variance constraint design for a class of stochastic large-scale uncertain time-delay systems. The considered time-delay parameters appear in the interconnections between individual subsystems and uncertainties are allowed to be unstructured but time-varying and normbounded. The sufficient conditions of the desired state feedback controller, which satisfies the performance level constraint in terms of H∝ norm for noise attenuation and upper bound of individual state variance constraint for considering its state energy limitation, are based on the LyapunovKrasovskii stability theory and utilizing the decentralized scheme to be derived in terms of linear matrix inequalities (LMIs). The effectiveness of the proposed approach is illustrated by a numerical example.ABSTRACT
Keywords:
LMI, Large-Scale Uncertain Time-Delay System, Robustly Decentralized Control, Variance Constraint
REFERENCES