Praveen Ailawalia This email address is being protected from spambots. You need JavaScript enabled to view it.¹ and Rajneesh Kumar²

¹Department of Mathematics, M. M. Engineering College, Maharishi Markandeshwar University, Mullana, District Ambala, Haryana, India
²Department of Mathematics, Kurukshetra University, Kurukshetra, Haryana, India, 136119

REFERENCES

1. [1] Biot, M., “Thermoelasticity and Irreversible Thermodynamics,” J. Appl. Phys., Vol. 27, pp. 240
   253 (1956).
2. [2] Lord, H. W. and Shulman, Y., “A Generalized Dynamical Theory of Thermoelasticity,” J. Mech. Phys. Solids, Vol. 15, pp. 299
   306 (1967).
3. [3] Muller, J., M., “The Coldness a Universal Function in Thermoelastic Bodies,” Arch. Ration. Mech. Anal., Vol. 41, pp. 319
   332 (1971).
4. [4] Green, A. E. and Laws, N., “On the Entropy Production Inequality,” Arch. Ration. Mech. Anal., Vol. 45, pp. 47
   53 (1972).
5. [5] Green, A. E. and Lindsay, K. A., “Thermoelasticity,” J. Elasticity, Vol. 2, pp. 1
   5 (1972).
6. [6] Suhubi, E, S., Thermoelastic solids in “A C Eringen (Ed.)” Continuum Physics, Vol. 2, Academic Press, Newyork, , Part 2, Chapter 2 (1975).
7. [7] Eringen, A. C., “Linear Theory of Micropolar Elasticity,” J. Math. Mech., Vol. 15, pp. 909
   923 (1966).
8. [8] Eringen, A. C., Foundations of Micropolar Thermoelasticity Course of Lectures No. 23, CISM Udine, Springer (1970).
9. [9] Nowacki, M., Couple-Stresses in the Theory of Thermoelasticity, Proc. IUTAM Symposia, Vienna, Editors H., Parkus and L. I Sedov, Springer-Verlag, pp. 259
   278 (1966).
10. [10] Iesan, D., “The Plane Micropolar Strain of Orthotropic Elastic Solids,” Arch. Mech., Vol. 25, pp. 547
    561 (1973).
11. [11] Iesan, D., “Torsion of Anisotropic Elastic Cylinders,” ZAMM, Vol. 54, pp. 773
    779 (1974).
12. [12] Iesan, D., “Bending of Orthotropic Micropolar Elastic Beams by Terminal Couples,” An. St. Uni. Iasi, Vol. XX, pp. 411
    418 (1974).
13. [13] Nakamura, S., Benedict, R. and Lakes, R., “Finite Element Method for Orthotropic Micropolar Elasticity,” Int. J. Engg. Sci., Vol. 22, pp. 319
    330 (1984).
14. [14] Kumar, R. and Choudhary, S., “Influence and Green’s Function for Orthotropic Micropolar Continua,” Archives of Mechanics, Vol. 54, pp. 185
    198 (2002).
15. [15] Kumar, R. and Choudhary, S., “Dynamical Behavior of Orthotropic Micropolar Elastic Medium,” Journal of Vibration and Control, Vol. 8, pp. 1053
    1069 (2002).
16. [16] Kumar, R. and Choudhary, S., “Mechanical Sources in Orthotropic Micropolar Continua,” Proc. Indian. Acad. Sci. (Earth Plant. Sci.), Vol. 111, pp. 133
    141 (2002).
17. [17] Kumar, R. and Choudhary, S., “Response of Orthotropic Micropolar Elastic Medium Due to Various Sources,” Meccanica, Vol. 38, pp. 349
    368 (2003).
18. [18] Kumar, R. and Choudhary, S., “Response of Orthotropic Micropolar Elastic Medium Due to Time Harmonic Sources,” Sadhana, Vol. 29, pp. 83
    92 (2004).
19. [19] Minagawa, S., Arakawa, K. and Yamada, M., “Dispersion Curves for Waves in a Cubic Micropolar Medium with Reference to Estimations of the Material Constants for Diamond,” Bull. JSME., Vol. 24, pp. 22
    28 (1981).
20. [20] Kumar, R. and Rani, L., “Elastodynamics of Time Harmonic Sources in a Thermally Conducting Cubic Crystal,” Int. J. Appl. Mech. Engg., Vol. 8, pp. 637
    650 (2003).
21. [21] Kumar, R. and Ailawalia, P., “Behaviour of Micropolar Cubic Crystal Due to Various Sources,” Journal of Sound and Vibration, Vol. 283, pp. 875
    890 (2005).
22. [22] Kumar, R. and Ailawalia, P., “Deformation in Micropolar Cubic Crystal Due to Various Sources,” Int. J. Solids. Struct., Vol. 42, pp. 5931
    5944 (2005).
23. [23] Kumar, R. and Ailawalia, P., “Mechanical/Thermal Sources at Thermoelastic Micropolar Medium without Energy Dissipation Possessing Cubic Symmetry,” International Journal of Thermophysics, Vol. 28, pp. 342
    367 (2007).
24. [24] Kumar, R. and Ailawalia, P., “Deformations in Micropolar Thermoelastic Medium Possessing Cubic Symmetry Due to Inclined Loads,” Mechanics of Advanced Materials and Structures, Vol. 15, pp. 64
    76 (2008).
25. [25] Kuo, J. T., “Static Response of a Multilayered Medium under Inclined Surface Loads,” J. Geophysical Research, Vol 74, pp. 3195
    3207 (1969).
26. [26] Garg, N. R., Kumar, R., Goel, A. and Miglani, A., “Plane Strain Deformation of an Orthotropic Elastic Medium Using Eigen Value Approach,” Earth Planets Space, Vol. 55, pp. 3
    9 (2003).
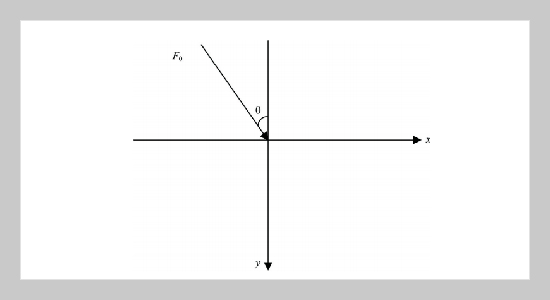
27. [27] Kumar, R. and Ailawalia, P. “Moving Inclined Load at Boundary Surface,” Applied Mathematics and Mechanics, Vol. 26, pp. 476
    485 (2005).
28. [28] Kumar, R. and Ailawalia, P. “Interactions Due to Inclined Load at Micropolar Elastic Half-Space with Voids,” Int. J. Appl. Mech. Engg., Vol. 10, pp. 109
    122 (2005).
29. [29] Press, W. H., Teukolsky, S. A., Vellerling, W. T. and Flannery, B. P., Numerical Recipes, Cambridge: Cambridge University Press (1986).
30. [30] Eringen, A. C., “Plane Waves in Non-Local Micropolar Elasticity,” Int. J. Engg. Sci., Vol. 22, pp. 1113
    1121 (1984).
31. [31] Dhaliwal, R. S. and Singh, A., Dynamic Coupled Thermoelasticity, p. 726, Hindustan Publication Corporation, New Delhi, India (1980).