Chi-Hau Chen This email address is being protected from spambots. You need JavaScript enabled to view it.1 and Uvais Qidwai This email address is being protected from spambots. You need JavaScript enabled to view it.2 1ECE Department University of Massachusetts, Dartmouth Massachusetts, U.S.A.
2EECS Department Tulane University, New Orleans, Louisiana, U.S.A.
Received:
October 25, 2001
Accepted:
February 19, 2002
Publication Date:
March 1, 2002
Download Citation:
||https://doi.org/10.6180/jase.2002.5.1.06
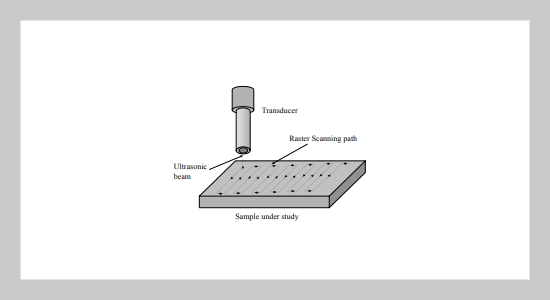
Ultrasonic imaging for nondestructive evaluation (NDE) applications is an important process for industrial applications. Understanding the material structure is an integral part of the manufacturing as well as maintenance operations. Especially for the critical industries like airlines where each component of the aircraft is required to perform at its best. One way to analyze material samples for defects is to take its x-ray image. This method is not only hazardous but also highly impractical to be used in many industrial applications specially during running conditions of structures. In addition, it is also very costly procedure. Ultrasonic imaging is an alternate for such application and is constantly gaining popularity in the industrial applications. Ultrasonic images are constrained by the sensor positions and indirect image formation. In this paper, some recent techniques in the areas of ultrasonic image enhancement and restoration, developed by the authors, are presented. Three new approaches have been presented to enhance the ultrasonic images with minimum or no information of the distortion function or the imaging system characteristics.ABSTRACT
Keywords:
Ultrasonic Images, Nondestructive Evaluation, H-Infinity Method, High-Order Statistics Algorithms, 2D-Deconvolution, Image Restoration
REFERENCES