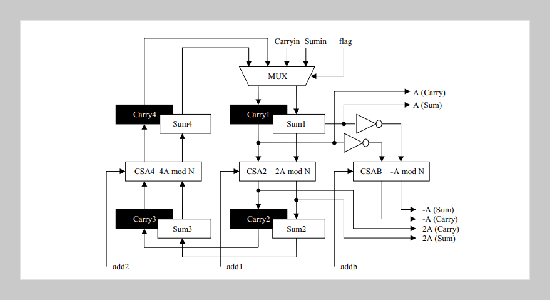
REFERENCES
- [1] Rivest, R. L., Shamir, A. and Adleman, L., “A Method for Obtaining Digital Signatures and Public-key Cryptosystems,” Com. of ACM, Vol. 21, pp. 120126 (1978).
- [2] Takagi, N. and Yajima, S., “Modular Multiplication Hardware Algorithms with a Redundant Representation and Their Application to Rsa Cryptosystem”, IEEE Trans. on Computers, Vol. 41, pp. 887891 (1992).
- [3] Wang, P. A., Tsai, W.-C. and Shung, C. B., “New VLSI Architecture of RSA Public-key Cryptosystem,” IEEE Int. Symp. on Circuits and Systems, Hong Kong, Vol. 3, pp. 20402043 (1997).
- [4] Chen, P.-S., Hwang, S.-A. and Wu, C.-W., “A Systolic RSA Public Key Cryptosystem,” IEEE Int. Symp. on Circuits and Systems, Atlanta, GA, U.S.A., Vol. 4, pp. 408411 (1996).
- [5] Jeong, Y.-J. and Burleson, W. P., “VLSI Array Algorithm and Architectures for Rsa Modular Multiplication,” IEEE Trans. on Very Large Scale Integration (VLSI) Systems, Vol. 5, pp. 211217 (1997).
- [6] Sheu, J.-L., Shieh, M.-D., Wu, C.-H. and Sheu, M.-H., “A Pipelined Architecture of Fast Modular Multiplication for Rsa Cryptography,” IEEE Int. Symp. on Circuits and Systems, Monterey, CA, U.S.A., Vol. 2, pp. 121124 (1998).
- [7] Eldridge, S. E., “A Faster Modular Multiplication Algorithm,” Int. J. Computer Math, Vol. 40, pp. 6368 (1991).
- [8] Su, C.-Y. and Wu, C.-W., “A Practical VLSI Architecture for Rsa Public-key Cryptosystem,” Proc. Sixth VLSI Design/CAD Symp., NanTou, Taiwan, pp. 273276, (1995).
- [9] Juang, Y.-J., Lee, E.-H. and Chen, C.-H., “A New Architecture for Fast Modular Multiplication,” Int. Symp. on VLSI Technology, System, and Application, pp. 357360 (1989).
- [10] Knuth, D. E., Seminumerical Algorithms, the Art of Computer Programming, Vol. 2, 2nd Ed. Reading, MA: Addison-Wesley, (1981).
- [11] Yang, C., “IC Design of a High Speed RSA Processor,” Master Thesis, Institute of Electronic, National Chiao Tung University, Hsin-Chu, Taiwan, June (1996).
- [12] Takagi, N., “A Radix-4 Modular Multiplication Hardware Algorithm Efficient for Iterative Modular Multiplcations,” 10th IEEE Symp. on Computer Arithmetic, Grenobal, France, pp. 3542, (1991).
- [13] Shand, M. and Vuillemin, J., “Fast Implementation of RAS Cryptograph,” 11th IEEE Symp. on Computer Arithmetic, Windsor, Ont., Canada, pp. 252259, (1993).
- [14] Kahn, D., The Codebreakers. NY, U.S.A., Macmillan, (1967).
- [15] Niven, I., Zuckerman, H. S. and Montgomery, H. L., An Introduction to the Theory of Numbers, Wiley, NY, U.S.A., (1991).
- [16] Orup, H., “Exponentiation, Modular Multiplication and VLSI implementation of High-Speed RSA Cryptosystem,” PhD dissertation, Dept. Comput. Sci., Univ. Aarhus, Arahus, Denmark (1995).
- [17] Montgomery, P. L., “Modular Multiplication without trial Division,” Math. Comput., Vol. 44, pp. 519521 (1985).
- [18] Su, C.-Y., Hwang, S.-A., Chen, P.-S. and Wu, C.-W., “An improved Montgomery’s Algorithm for HighSpeed RSA Public-Key Cryptosystem,” IEEE Trans. on Very Large Scale Integration (VLSI) System, Vol. 7, pp. 280284 (1999).
- [19] Chiang, J.-S. and Chen, J.-K., “An Efficient VLSI Architecture for RSA Public-Key Cryptosystem,” IEEE Int. Symp. on Circuits and Systems, Orlando, FL, U.S.A., Vol. 2, pp. 121124 (1999).
- [20] Ishii, S., Ohyama, K. and Yamanaka, K., “A Signal-chip RSA Processor Implemented in a 0.5 �m Rule Gate Array” IEEE International ASIC conference and Exhibit, pp. 433436 (1994).
- [21] Holger, Orup “A 100 K bits/s Signal Chip Modular Exponentation Processor,” In HOT Chips VI, Symposium Record, pp. 5359 (1994).
- [22] Chen, P.-S., Hwang S.-A. and Wu, C.-W., “A Systolic RSA Public Key Cryptosystem,” IEEE International Symposium Circuits and Systems, Vol. 4, pp. 408411 (1996).