Chin-Hwa Kuo¹ , Tzu-Chuan Chou This email address is being protected from spambots. You need JavaScript enabled to view it.² and Meng-Chang Chen²

¹Department of Computer Science and Information Engineering, Tamkang University, Tamsui, Taiwan 251, R.O.C
²Institute of Information Science, Academia Sinica, Taipei, Taiwan 115, R.O.C.

REFERENCES

1. [1] Moon, Todd K., “The Expectation-Maximization Algorithm,” IEEE Signal Processing Magazine, pp. 47
   60 (1996).
2. [2] Dempster, A. P., Laird, N. M. and Rubin, D. B., “Maximum Likelihood from Incomplete Data via the EM Algorithm,” Journal of the Royal Statistical Society Series B, Vol. 39, pp. 1
   38 (1977).
3. [3] Bilmes, Jeff A. “A Gentle Tutorial of the EM Algorithm and its Application to Parameter Estimation for Gaussian Mixture and Hidden Markov Models,” Technical Report TR-97-021, Computer Science Division, Department of Electrical Engineering and Computer Science, U. C. Berkeley (1998).
4. [4] Ball, G. and Hall, D. “A Clustering Technique for Summarizing Multivariate Data,” Behavioral Science, Vol. 12, pp. 153
   155 (1967).
5. [5] Dunn, J. C., “A Fuzzy Relative of the ISODATA Process and its Use in Detecting Compact Well-separated Clusters,” Journal Cybernetics, Vol. 3, pp. 95
   104 (1974).
6. [6] Frank Hoppner, Frank Klawonn, Rudolf Kruse and Thomas Runkler, Fuzzy Cluster Analysis, Methods for Classification, Data Analysis and Image Recognition, Wiley, New York, U.S.A. (2000).
7. [7] Bezdek, James C., Pattern Recognition with Fuzzy Objective Function Algorithm. Plenum, New York, U.S.A. (1981).
8. [8] Gustafson, Donald E. and Kessel, William C., “Fuzzy Clustering with a Fuzzy Covariance Matrix,” In Proc. of the IEEE Conference on Decision and Control, pp. 761
   766 (1979).
9. [9] Isak Gath and Geva, Amir. B., “Unsupervised Optimal Fuzzy Clustering,” IEEE Trans. Pattern Analysis and Machine Intelligence, Vol. 11, pp. 773
   781 (1989).
10. [10] Jorma Rissanen, “Modeling by Shortest Data Description,” Automatica, Vol. 14, pp. 465
    471 (1978).
11. [11] Gideon Schwarz, “Estimating the Dimension of a Model,” The Annals of Statistics, Vol. 6, pp. 461
    464 (1978).
12. [12] Chris Fraley and Raftery, Adrian E., “How Many Clusters? Which Clustering Method? Answers via Modelbased Cluster Analysis,” The Computer Journal, Vol. 41, pp. 578
    588 (1998).
13. [13] Peter Cheeseman and John Stutz, Bayesian Classification (AutoClass): Theory and Results, In U. Fayyad, G. Piatetsky-Shapiro, P. Smyth and U. Uthurusamy, Advances in Knowledge Discovery and Data Mining, AAAI Press/MIT Press. 153
    180 (1996).
14. [14] Pal, Nikhil R. and Bezdek, James C., “On Cluster Vaidity for the Fuzzy c-means Model,” IEEE Trans. Fuzzy Systems, Vol. 3, pp. 370
    379 (1995).
15. [15] Lawrence O. Hall, Ibrahim Burak Ozyurt, and Bezdek, James C., “Clustering with a Genetically Optimized Approach,” IEEE Transactions on Evolutionary Computation, Vol. 3, pp. 103
    112 (1999).
16. [16] Nir Friedman, Matan Ninio, Itsik Pe’er, and Tal Pupko, “A Structural EM Algorithm for Phylogenetic Inference,” Journal of Computational Biology. Vol. 9, pp. 331
    353 (2002).
17. [17] Schachter, B., Davis, L. and Rosenfeld, A., “Some Experiments in Image Segmentation by Clustering of Local Feature Values,” Pattern Recognition, Vol. 11, pp. 19
    28 (1979).
18. [18] Naonori Ueda, Ryohei Nakano, Zoubin Ghahramani and Hinton, Geoffrey E. “SMEM Algorithm for Mixture Models,” Neural Computation, Vol. 12, pp. 2109
    2128 (2000).
19. [19] Nikos Vlassis and Aristidis Likas, “A Greedy EM Algorithm for Gaussian Mixture Learning,” Neural Processing Letters, Vol. 15, pp. 77
    87 (2002).
20. [20] Henry. C. Thode, Jr., Stephen J. Finch and Nancy R. Mendell, “Simulated Percentage Points for the Null Distribution of the Likelihood Ratio Test for a Mixture of Two Normals,” Biometrics, Vol. 44, pp. 1195
    1201 (1988).
21. [21] Richard A. Johnson and Dean W. Wichern, Applied Multivariate Statistical Analysis, Third Edition, Prentice-Hall (1992).
22. [22] Sergios Theodoridis and Konstantinos Koutroumbas, Pattern Recognition, Academic Press (1999).
23. [23] Gentle, James E. Random Number Generation and Monte Carlo Methods, Springer (1998).
24. [24] William H. Press, Brian P. Flannery, Saul A. Teukolsk and William T., Vetterling, Numerical recipes in C, Cambridge University Press (1988).
25. [25] Yoav Freund and Yishay Mansour, “Estimating a Mixture of Two Product Distributions,” ACM Conference on Computational Learning Theory, pp. 53
    59 (1999).
26. [26] Blake, C. L. and Merz, C. J., “UCI Repository of Machine Learning Databases,” University of California, Irvine, Department of Information and Computer Sciences (1998).
27. [27] Aeberhard, S., Coomans, D. and de Vel, O., “Comparison of Classifiers in High Dimensional Settings,” Technical Report No. 92
    02, (1992), Department of Computer Science and Department of Mathematics and Statistics, James Cook University of North Queensland (1992).
28. [28] Aeberhard, S., Coomans, D. and de Vel, O., “The Classification Performance of RDA,” Technical Report No. 92
    01, (1992), Department of Computer Science and Department of Mathematics and Statistics, James Cook University of North Queensland (1992).
29. [29] Soumen Chakrabarti, Mining the Web, Discovering Knowledge from Hypertext Data, Morgan Kaufmann Publishers (2003).
30. [30] Zhihua Zhang, Chibiao Chen, Jian Sun and Kap Luk Chan, “EM Algorithms for Learning Gaussian Mixture Models with Split-and-Merge Operation,” Pattern Recognition, Vol. 36, pp. 1973
    1983 (2003).
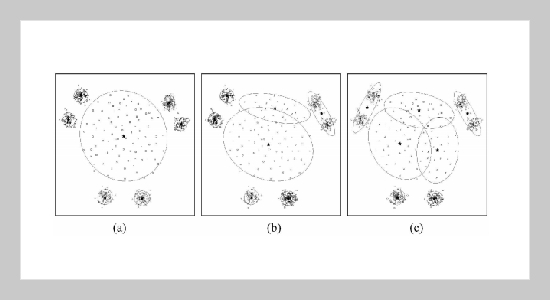
31. [31] Tao, C. W. “Unsupervised Fuzzy Clustering with Multi-center Clusters,” Fuzzy Sets and Systems, Vol. 128, pp. 305
    322 (2002).
32. [32] Asa Ben-Hur, David Horn, Hava T. Siegelmann and Vladimir Vapnik. “Support Vector Clustering,” Journal of Machine Learning Research, Vol. 2, pp. 125
    137 (2002).