REFERENCES
- [1] Chadwick, P., Thermoelasticity, the Dynamic Theory, Progress in Solid Mechanics, Vol. 1 (Sneddon, I. N., Hill. R., eds.), p. 265, Amsterdam: North-Holland (1960).
- [2] Lord, H. W. and Shulman, Y., “AGeneralized Dynamical Theory of Thermoelasticity,” J. Mech. Phys. Solids, Vol. 15, pp. 299�309 (1967).
- [3] Green, A. E. and Lindsay, K. A., “Thermoelasticity,” J. Elasticity, Vol. 2, pp. 1�7 (1972).
- [4] Chandrasekharaiah, D. S., “Thermoelasticity with Second Sound: A Review,” Appl. Mech. Rev. Vol. 39, pp. 355�376 (1986).
- [5] Ignaczak, J., Generalized Thermoelasticity and its Applications. In: Thermal stresses, Vol. III (Hetnarski, R. B. ed.). Chapter 4. Oxford: Elsevier (1989).
- [6] Joseph, D. D. and Preziosi, L., “Heat Waves,” Revs. Mod. Phys. Vol. 61, pp. 41�73 (1989) and addendum Vol. 62, pp. 375�391 (1990).
- [7] Green, A. E. and Naghdi, P. M., “A Re-Examination of the Basic Postulates of Thermomechanics,” Proc. R. Soc. London, Ser. A, Vol. 432, pp. 171�194 (1991).
- [8] Green, A. E. and Naghdi, P. M., “On Undamed Heat Waves in Elastic Solid,” J. Thermal Stresses, Vol. 15, pp. 253�264 (1992).
- [9] Green, A. E. and Naghdi, P. M., “Thermoelasticity without Energy Dissipation,” J. Elasticity, Vol. 31, pp. 189�208 (1993).
- [10] Green, A. E. and Naghdi, P. M., “A Unified Procedure for Construction of Theories of Deformable Media. I. Classical Continuum Physics, II. Generalized Continua, III. Mixtures of Interacting Continua,” Proc. R. Soc. London A, Vol. 448, pp. 335�356, 357�377, 379�388 (1995).
- [11] Chandrasekharaiah, D. S., “A Note on the Uniqueness of Solution in the Linear Theory of Thermoelasticity without Energy Dissipation,” J. Elasticity, Vol. 43, pp. 279�283 (1996).
- [12] Chandrasekharaiah, D. S., “A Uniqueness Theorem in the Theory of Thermoelasticity without Energy Dissipation,” J. Thermal Stresses, Vol. 19, pp. 267�272 (1996).
- [13] Li, H. and Dhaliwal, R. S., “Thermal Shock Problem in Thermoelasticity without Energy Dissipation,” Indian J. pure appl. Math., Vol. 27, pp. 85�101 (1996).
- [14] Scott, N. H., “Energy and Dissipation of Inhomogeneous Plane Waves in Thermoelasticity,” Wave motion, Vol. 23, pp. 393�406 (1996).
- [15] Chandrasekharaiah, D. S. and Srinath, K. S., “Axisymmetric Thermoelastic Interaction without Energy Dissipation in an Unbounded Body with Cylindrical Cavity,” J. Elasticity, Vol. 46, pp. 19�31 (1997).
- [16] Chandrasekharaiah, D. S. and Srinath, K. S., “Thermoelastic Waves without Energy Dissipation in an Unbounded Body with Spherical Cavity,” Internat. J. Math and Math. Sci., Vol. 23, pp. 555�562 (2000).
- [17] Iesan, D., “On the Theory of Thermoelasticity without Energy Dissipation,” J. Thermal Stresses, Vol. 21, pp. 295�307 (1998).
- [18] Quintanilla, R., “On the Spatial Behaviour in Thermoelasticity without Energy Dissipation,” J. Thermal Stresses, Vol. 22, pp. 213�224 (1999).
- [19] Quintanilla, R., “Instability, Non-existence in the Nonlinear Theory of Thermoelasticity without Energy Dissipation,” Continuum Mech. Thermodyn., Vol. 13, pp. 121�129 (2001).
- [20] Quintanilla, R., “On Existence in Thermoelasticity without Energy Dissipation,” J. Thermal Stresses, Vol. 25, pp. 195�202 (2002).
- [21] Wang, J. and Slattery, S. P., “Thermoelasticity without Energy Dissipation for Initially Stressed Bodies,” International Journal of Mathematics and Mathematical Sciences, Vol. 31, pp. 329�337 (2002).
- [22] Quintanilla, R., “Thermoelasticity without Energy Dissipation of Nonsimple Materials.” Jour. Appl. Mathematics Mechanics (ZAMM), Vol. 83, pp. 172�180 (2003).
- [23] Love, A. E. H., A Treatise on the Mathematical Theory of Elasticity, Dover Publications, New York, U.S.A. (1944).
- [24] Maruyama, T., “On Two-Dimensional Elastic Dislocations in an Infinite and Semi-Infinite Medium,” Bull. Earthq. Res. Inst. Vol. 44, pp. 811�871 (1966).
- [25] Okada, Y., “Surface Deformation due to Inclined Shear and Tensile Faults in a Homogeneous Isotropic HalfSpace,” Bull. Seismol. Soc. Am. Vol. 75, pp. 1135�1154 (1985).
- [26] Okada, Y., “Internal Deformation due to Shear and Tensile Faults in a Half-Space,” Bull. Seismol. Soc. Am. Vol. 82, pp. 1018�1040 (1992).
- [27] Kuo, J. T., “Static Response of a Multilayered Medium under Inclined Surface Loads,” Journal of Geophysical research, Vol. 74, pp. 3195�3207 (1969).
- [28] Gerstle, F. P. and Pearsall, G. W., “The Stress Response of an Elastic Surface to a High Velocity, Unlubricated Punch,” ASME Jounal of Applied Mechanics, Vol. 41, pp. 1036�1040 (1974).
- [29] Kumar, R., Miglani, A. and Garg, N. R., “Plane Strain Problem of Poroelasticity using Eigenvalue Approach,” Proceeding Indian Acad. Sci. (Earth Planet Sci.), Vol. 109, pp. 371�380 (2000).
- [30] Kumar, R., Miglani, A. and Garg, N. R., “Response of an Anisotropic Liquid-Saturated Porous Medium due to Two-Dimensional Sources,” Proceeding Indian Acad. Sci. (Earth Planet Sci.), Vol. 111, pp. 143�151 (2002).
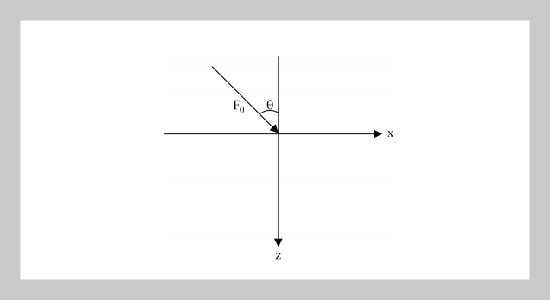
- [31] Kumar, R. and Rani, L., “Response of Thermoelastic Half-Space with Voids due to Inclined Load,” (Accepted for publication in International Journal of Applied Mechanics and Engineering, IJAME, POLAND).
- [32] Kumar, R. and Rani, L., “Deformation due to Inclined Load in Thermoelastic Half-Space with Voids,” Archives of Mechanics, POLAND, Vol. 57, pp. 7�24 (2005)
- [33] Honig, G. and Hirdes, U., “A Method for the Numerical Inversion of Laplace Transform,” Journal of Computational and Applied Mathematics, Vol. 10, pp. 113�132 (1984).
- [34] Press,W. H., Teukolshy, S. A., Vellerling, W. T. and Flannery, B. P., Numerical Recipes in FORTRAN (2nd edn.), Cambridge University Press, Cambridge (1986).
- [35] Dhaliwal, R. S. and Singh, A., Dynamic Coupled Thermoelasticity, p. 726, Hindustan Publ. Corp., New Delhi, India (1980).