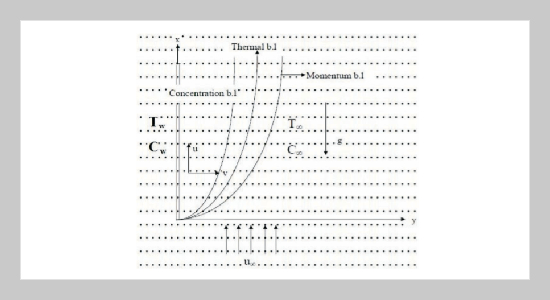
REFERENCES
- [1] Nield, D. A. and Bejan, A., Convection in Porous Media, Springer-Verlag, New York (2006).
- [2] Eckeret, E. R. G. and Drake, R. M., Analysis of Heat and Mass Transfer, McGraw Hill, Newyark (1972).
- [3] Kafoussias, N. G., “Local Similarity Solution for Combined Free-Forced Convective and Mass Transfer Flow Past a Semi-Infinite Vertical Plate,” Int. J. Energy Res., Vol. 14, pp. 305�309 (1990).
- [4] Dursunkaya, Z. and Worek, W. M., “Diffusion-Thermo and Thermal Diffusion Effects in Transient and Steady Natural Convection from a Vertical Surface,” Int. J. Heat Mass Transfer, Vol. 35, pp. 2060�2065 (1992).
- [5] Kafoussias, N. G. and Williams, N. G., “Thermal-Diffusion and Diffusion-Thermo Effects on Mixed FreeForced Convective and Mass Transfer Boundary Layer Flow with Temperature Dependent Viscosity,” Int. J. Engng. Sci., Vol. 33, pp. 1369�1384 (1995).
- [6] Postelnicu, A., “Influence of a Magnetic Field on Heat and Mass Transfer by Natural Convection from Vertical Sufaces in Porous Media Considering Soret and Dufour Effects,” Int. J. Heat Mass Transfer, Vol. 47, pp. 1467�1475 (2004).
- [7] Alam, M. S. and Rahman, M. M., “Dufour and Soret Effects on Mixed Convection Flow Past a Vertical Porous Flat Plate with Variable Suction,” Nonlinear Analysis: Modeling and Control, Vol. 11, pp. 3�12 (2006).
- [8] Abreu, C. R. A., Alfradique, M. F. and Silva, A. T., “Boundary Layer Flows with Dufour and Soret Effects: I: Forced and Natural Convection,” Chemical Engineering Science, Vol. 61, pp. 4282�4289 (2007).
- [9] Lakshmi Narayana, P. A. and Murthy, P. V. S. N., “Soret and Dufour Effects in a Doubly Stratified Darcy Porous Medium,” Journal of Porous Media, Vol. 10, pp. 613�624 (2007).
- [10] Srinivasacharya, D. and RamReddy, Ch., “Soret and Dufour Effects on Mixed convection in a Non-Darcy Porous Medium Saturated with Micropolar Fluid,” Nonlinear Analysis: Modelling and Control, Vol. 16, pp. 100�115 (2011).
- [11] Stokes, V. K., “Couple Stresses in Fluid,” The Physics of Fluids, Vol. 9, pp. 1709�1715 (1966).
- [12] Srivastava, L. M., “Peristaltic Transport of a CoupleStress Fluid,” Rheol, Acta, Vol. 25, pp. 638�641 (1986).
- [13] Shehawey, E. F. E. and Mekheimer, K. S., “CoupleStresses in Peristaltic Transport of Fluids,” J. Phys. D. Appl. Phys., Vol. 27, pp. 1163�1170 (1994).
- [14] Dulal Pal, Rudraiah, L. M. and Devanathan, R., “A Couple Stress Model of Blood Flow in the Microcirculation,” Bull. Math. Biol., Vol. 50, pp. 329�344 (1988).
- [15] Chiang, H. L., Hsu, C. H. and Lin, J. R., “Lubrication Performance of Finite Journal Bearings Considering Effects of Couple Stresses and Surface Roughness,” Tribol. Int., Vol. 37, pp. 297�307 (2004).
- [16] Naduvinamani, N. B., Hiremath, P. S. and Gurubasavaraj, G., “Effect of Surface Roughness on the Couple-Stress Squeeze Filmbetween a Sphere and a Flat Plate,” Tribol. Int., Vol. 38, pp. 451�458 (2005).
- [17] Jian, C. W., Chang, and Chen, C. K., “Chaos and Bifurcation of a Flexible Rotor Supported by Porous Squeeze Couple Stress Fluid Film Journal Bearings with Non-Linear Suspension,” Chaos, Solitons Fractals, Vol. 35, pp. 358�375 (2006).
- [18] Lu, R. F. and Lin, J. R., “A Theoretical Study of Combined Effects of Non-Newtonian Rheology and Viscosity Pressure Dependence in the Sphere-Plate Squeeze-Film System,” Tribol. Int., Vol. 40, pp. 125� 131 (2007).
- [19] Srinivasacharya, D. and Kaladhar, K., “Mixed Convection Flow of Couple Stress Fluid between Parallel Vertical Plates with Hall and Ion-Slip Effects,” Commun Nonlinear Sci Numer Simulat., Vol. 17, pp. 2447� 2462 (2012).
- [20] Cebeci, T. and Bradshaw, P., Physical and Computational Aspects of Convective Heat Transfer, SpringerVerlag, New York (1988).
- [21] McDougall, T. J., “Double Diffusive Convection Caused by Coupled Molecular Diffusion,” J. Fluid Mech., Vol. 126, pp. 379�397 (1982).