Yuh-Chung Hu This email address is being protected from spambots. You need JavaScript enabled to view it.¹ and Guan-De Lee¹

¹Advanced Manufacturing Research Center & Department of Mechatronic Engineering, Huafan University, Taipei, Taiwan 223, R.O.C.

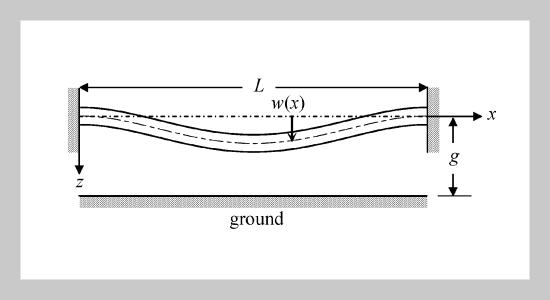
REFERENCES

1. [1] Osterberg, P. M. and Senturia, S. D., “M-TEST: A Test Chip for MEMS Material Property Measurement Using Electrostatically Actuated Test Structures,” Journal of Microelectromechanical Systems, Vol. 6, pp. 107
   118 (1997).
2. [2] Gupta, R. K., “Electrostatic Pull-in Test Structures Design for in-situ Mechanical Property Measurement of Microelectromechanical Systems (MEMS),” Ph.D. Dissertation, MIT, MA, USA (1997).
3. [3] Hu, Y. C., Chang, C. M. and Huang, S. C., “Some Design Considerations on the Electrostatically Actuated Microstructures,” Sensors and Actuators A: Physical Vol. 112, pp. 155
   161 (2004).
4. [4] Hu, Y. C., Wang, Y. H. and Huang, S. C., “On the Dynamic and Stability Analysis of Electrostatically Actuated Microstructures,” Proceedings of the 1st International Symposium on Micro & Nano Technology (ISMNT-1), Honolulu, Hawaii, Vol. III-2-01 (2004).
5. [5] Hu, Y. C. and Tu, W. H., “Non-Linear and Linearized Algorithms for the Young’s Modulus Extraction of Thin Films through the C-V measurement of Microstructures,” Journal of Applied Physics, Vol. 98, p. 104504 (2005).
6. [6] Osterberg, P., Yie, H., Cai, X., White, J. and Senturia, S. D., “Self-Consistent Simulation and Modeling of Electrostatically Deformed Diaphragms,” Proceedings of the IEEE MEMS’94 Workshop, Osio, Japan, pp. 28
   32 (1994).
7. [7] Pamidighantam, S., Puers, R., Baert, K. and Tilmans, H. A. C., “Pull-in Voltage Analysis of Electrostatically Actuated Beam Structures with Fixed-Fixed and FixedFree End Conditions,” Journal of Micromechanics and Microengineering, Vol. 12, pp. 458
   464 (2002).
8. [8] Cheng, J., Zhe, J. and Wu, X., “Analytical and Finite Element Model Pull-in Study of Rigid and Deformable Electrostatic Microactuators,” Journal of Micromechanics and Microengineering, Vol. 14, pp. 57
   68 (2004).
9. [9] Chowdhery, S., Ahmadi, M. and Miller, W. C., “A Closed-Form Model for the Pull-in Voltage of Electrostatically Actuated Cantilever Beams,” Journal of Micromechanics and Microengineering, Vol. 15, pp. 756
   763 (2005).
10. [10] Lin, H. H., Chu, C. H., Chang, C. L. and Chang, P. Z., “Mechanical Behavior of RF MEMS,” Proceedings of the Second International Symposium on Acoustic Wave Devices for Future Mobile Communication Systems, Chiba University, Japan, pp. 121
    125 (2004).
11. [11] Petersen, K. E., “Dynamic Micromechanics on Silicon Techniques and Devices,” IEEE Transactions on Electron Devices, Vol. ED-25, pp. 1241
    1250 (1978).
12. [12] Wei, L. C., Mohammad, A. B. and Kassim, N. M., “Analytical Modeling for Determination of Pull-in Voltage for an Electrostatic Actuated MEMS Cantilever Beam,” Proceedings of the IEEE ISCE 2002, Orlando, Florida, USA, pp. 233
    238 (2002).
13. [13] Legtenberg, R., Gilbert, J., Senturia, S. D. and Elwenspoek, M., “Electrostatic Curved Electrode Actuators,” Journal of Microelectromechanical Systems, Vol. 6, pp. 257
    265 (1997).
14. [14] Lee, B. C. and Kim, E. S., “Analysis of Partly Corrugated Rectangular Diaphragms Using the RayleighRitz Method,” Journal of Microelectromechanical Systems, Vol. 9, pp. 399
    406 (2000).
15. [15] Chen, J., Kang, S. M., Zou, J. and Liu, C., “Reducedorder Modeling of Weakly Nonlinear MEMS Devices with Taylor-series Expansion and Arnoldi Approach,” Journal of Microelecrtomechanical Systems, Vol. 13, pp. 441
    451 (2004).
16. [16] Leus, V. and Elata, D., Fringing Field Effect in Electrostatic Actuators, Israel Institute of Technology, Technical Report ETR-2004-2 (2004).