Chung-I Chang This email address is being protected from spambots. You need JavaScript enabled to view it.1, Nancy P. Lin2 and Nien-Yi Jan2,3 1Department of Information Management, St. Mary’s Medicine, Nursing and Management College
2Department of Computer Science and Information Engineering, Tamkang University, Tamsui, Taiwan 251, R.O.C
3Business & Marketing Strategy Research Department, Telecommunication Lab., Chunghwa Telecom Co., Ltd Taiwan, R.O.C.
Received:
November 21, 2007
Accepted:
July 24, 2008
Publication Date:
June 1, 2009
Download Citation:
||https://doi.org/10.6180/jase.2009.12.2.10
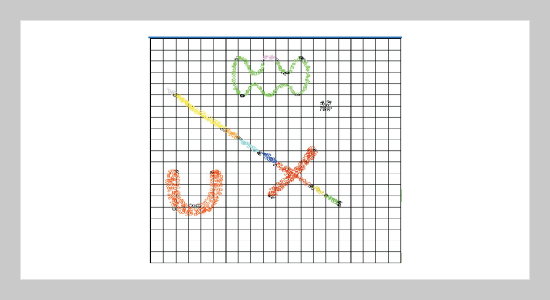
These spatial clustering methods can be classified into four categories: partitioning method, hierarchical method, density-based method and grid-based method. The grid-based clustering algorithm, which partitions the data space into a finite number of cells to form a grid structure and then performs all clustering operations to group similar spatial objects into classes on this obtained grid structure, is an efficient clustering algorithm. To cluster efficiently and simultaneously, to reduce the influences of the size and borders of the cells, a new grid-based clustering algorithm, an Axis-Shifted Grid-Clustering algorithm (ASGC), is proposed in this paper. This new clustering method combines a novel density-grid based clustering with axis-shifted partitioning strategy to identify areas of high density in the input data space. The main idea is to shift the original grid structure in each dimension of the data space after the clusters generated from this original structure have been obtained. The shifted grid structure can be considered as a dynamic adjustment of the size of the original cells and reduce the weakness of borders of cells. And thus, the clusters generated from this shifted grid structure can be used to revise the originally obtained clusters. The experimental results verify that, indeed, the effect of this new algorithm is less influenced by the size of cells than other grid-based ones and requires at most a single scan through the data.ABSTRACT
Keywords:
Data Mining, Grid-Based Clustering, Significant Cell, Grid Structure, Coordinate Axis
REFERENCES