Wei Chien1 , Chi-Hsien Sun2 and Ming-Hung Wu This email address is being protected from spambots. You need JavaScript enabled to view it.3
1Department of Electronic Engineering, De Lin Institute of Technology, Tucheng, Taiwan 236, R.O.C.
2Department of Electrical Engineering, Tamkang University, Tamsui, Taiwan 251, R.O.C.
3Department of Information Management, Cardinal Tien College of Healthcare & Management, Taipei, Taiwan 231, R.O.C.
REFERENCES
- [1]Roger, “Newton-Kantorovitch algorithm applied to an electromagnetic inverse problem,” IEEE Trans. Antennas Propagat., vol. AP-29, pp. 232-238, Mar. 1981.
- [2]C. C. Chiu and Y. W. Kiang, “Inverse scattering of a buried conducting cylinder,” Inverse Problems, vol. 7, pp. 187-202, April 1991.
- [3]C. C. Chiu and Y. W. Kiang, “Microwave imaging of multiple conducting cylinders,” IEEE Trans. Antennas Propagat., vol. 40, pp. 933-941, Aug. 1992.
- [4]P. Otto and W. C. Chew, “Microwave inverse scattering-local shape function imaging for improved resolution of strong scatterers.” IEEE Trans. Microwave Theory Tech., vol. 42, pp. 137-142, Jan. 1994.
- [5]Kress R, “A Newton method in inverse obstacle scattering Inverse Problem in Engineering Mechanics,” ed H D Bui et al (Rotterdam: Balkema), pp. 425-432, 1994
- [6]Colton and P. Monk, “A novel method for solving the inverse scattering problem for time-harmonic acoustic waves in the resonance region II,” SIAM J. Appl. Math., vol. 46, pp. 506-523, June 1986
- [7]Kirsch, R. Kress, P. Monk, and A. Zinn, “Two methods for solving the inverse acoustic scattering problem, “ Inverse problems, vol. 4, pp. 749-770, Aug. 1998.
- [8]Hettlich, “Two methods for solving an inverse conductive scattering problem,” Inverse Problems, vol. 10, pp. 375-385, 1994.
- [9]E. Kleinman and P.M. van den Berg, “Two-dimensional location and shape reconstruction,” Radio Sci., vol. 29, pp. 1157-1169,July-Aug. 1994.
- [10]Hohage T, “Iterative methods in inverse obstacle scattering: regularization theory of linear and nonlinear exponentially ill-posed problems,” Dissertation Linz, 1999.
- [11]E. Goldgreg, Genetic Algorithm in Search, Optimization and Machine Learning, Addison-Wesley, 1989.
- [12]C. Chiu and P. T. Liu, “Image reconstruction of a perfectly conducting cylinder by the genetic algorithm”, IEE Proc. Microw. Antennas Propag., vol. 143, pp. 249-253, June 1996.
- [13]Xiao and H. Yabe, “Microwave imaging of perfectly conducting cylinders from real data by micro genetic algorithm couple with deterministic method”, IEICE Trans. Electron., vol. E81-C, pp. Dec. 1998.
- [14]Q. Meng, T. Takenaka and T. Tanaka, “Image reconstruction of two- dimensional impenetrable objects using genetic algorithm”, Journal of Electromagnetic Waves and Applications, vol. 13, pp. 95-118, 1999.
- [15]Zuping Qian, Zhenyu Ding and Wei Hong, “Application of genetic algorithm and boundary element method to electromagnetic imaging of two-dimensional conducting targets”, 5th International Symposium on ISAPE, pp. 211-214, 2000.
- [16]L. Li, S.H. Chen, C. M. Yang, and C. C. Chiu, “Image reconstruction for a patially immersed perfectly conducting cylinder using the steady state algorithm,” Radio Science, vol.39, RS2016, April 2004.
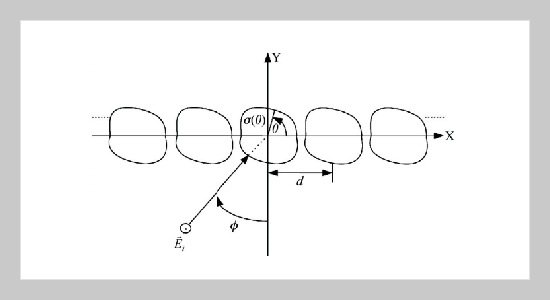
- [17]E. Jorgenson and R. Mittra, “Efficient calculation of free-space periodic Green’s function,” IEEE Trans. Antenna Propagat., vol. 38, pp. 633-642, May 1990.
- [18]S. Wallinga, E. J. Rothwell, K. M. Chen, and D. P. Nyquist, “Efficient computation of the two-dimensional periodic Green’s function,” IEEE Tran. Antenna Propagat., vol. 47, pp. 895-897, May 1999.
- [19]E. Goldgerg, Genetic Algorithm in Search, Optimization and Machine Learning. Addison-Wesley, 1989.