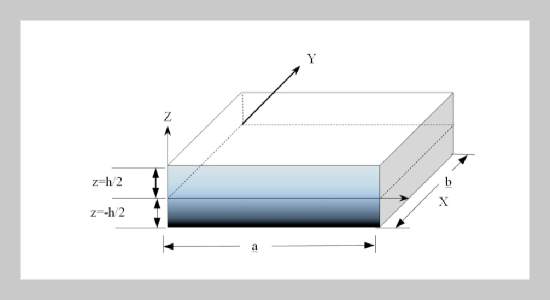
REFERENCES
- [1] Mantari, J. L. and Guedes Soares, C., “A Novel Higher-Order Shear Deformation Theory with Stretching Effect for Functionally Graded Plates,” Composites: Part B, Vol. 45, pp. 268�281 (2013). doi: 10.1016/j.compositesb.2013.07.027
- [2] Reddy, J. N. and Chin, C. D., “Thermomechanical Analysis of Functionally Graded Cylinders and Plates,” Journal of Thermal Stresses, Vol. 21, No. 6, pp. 593� 626 (1998). doi: 10.1080/01495739808956165
- [3] Reddy, J. N., “Analysis of Functionally Graded Plates,” International Journal for Numerical Methods in Engineering, Vol. 47, pp. 663�684 (2000).
- [4] Vel, S. S. and Batra, R. C., “Exact Solutions for Thermoelastic Deformations of Functionally Graded Thick Rectangular Plates,” AIAA Journal, Vol. 40, pp. 1421� 1433 (2002). doi: 10.2514/2.1805
- [5] Vel, S. S. and Batra, R., “Three Dimensional Analysis of Transient Thermal Stresses in Functionally Graded Plates,” International Journal of Solids and Structures, Vol. 40, No. 25, pp. 7181�7196 (2003). doi: 10.1016/S0020-7683(03)00361-5
- [6] Cheng, Z. Q. and Batra, R. C., “Three Dimensional Thermoelastic Deformations of a Functionally GradedEliptic Plate,” Composites: Part B, Vol. 31, pp. 97� 106 (2000). doi: 10.1016/S1359-8368(99)00069-4
- [7] Javaheri, R. and Eslami, Mr., “Thermal Buckling of Functionally Graded Plates Based on Higher Order Shear Deformation Theory,” Journal of Thermal Stresses, Vol. 25, No.7, pp. 603�625 (2002). doi: 10.1080/01495730290074333
- [8] Reissner, E., “The Effect of Transverse Shear Deformation on the Bending of Elastic Plates,” ASME Journal of Applied Mechanics, Vol. 12, No. 2, pp. 69�77 (1945).
- [9] Mindlin, R. D., “Influence of Rotary Inertia and Shear on Flexural Motions of Isotropic, Elastic Plates,” ASME Journal of Applied Mechanics, Vol. 18, pp. 31�38 (1951).
- [10] Thai, H. T. and Thuc, P. Vo., “A New Sinusoidal Shear Deformation Theory for Bending, Buckling, and Vibration of Functionally Graded Paltes,” Applied Mathematical Modelling, Vol. 37, pp. 3269�3281 (2013). doi: 10.1016/j.apm.2012.08.008
- [11] Zenkour, A. M., “A Comprehensive Analysis of Functionally Graded Sandwich Plates: Part-1-Deflection and Stresses,” International Journal of Solids and Structures, Vol. 42, No. 18�19, pp. 5224�5242 (2005). doi: 10.1016/j.ijsolstr.2005.02.015
- [12] Zenkour, A. M., “A Comprehensive Analysis of Functionally Graded Sandwich Plates: Part-2-Buckling and Free Vibration,” International Journal of Solids and Structures, Vol. 42, No. 18�19, pp. 5243�5258 (2005). doi: 10.1016/j.ijsolstr.2005.02.016
- [13] Zenkour, A. M., “Generalized Shear Deformation Theory for Bending Analysis of Functionally Graded Plates,” Applied Mathematical Modelling, Vol. 30, No. 1, pp. 67�84 (2006). doi: 10.1016/j.apm.2005.03.009
- [14] Kant, T., Owen, D. R. J. and Zienkiewicz, O. C., “A Refined Higher Order C0 Plate Element,” Computers and Structures, Vol. 15, No. 2, pp. 177�183 (1982). doi: 10.1016/0045-7949(82)90065-7
- [15] Pandya, B. N. and Kant, T., “Higher-Order Shear Deformable Theories for Flexure of Sandwich PlatesFinite Element Evaluations,” International Journal of Solids and Structures, Vol. 24, No. 12, pp. 1267�1286 (1988). doi: 10.1016/0020-7683(88)90090-X
- [16] Pandya, B. N. and Kant, T., “Finite Element Analysis of Laminated Composite Plates Using a Higher Order Displacement Model,” Composites Science and Technology, Vol. 32, No. 2, pp. 137�155 (1988). doi: 10.1016/0266-3538(88)90003-6
- [17] Kant, T. and Swaminathan, K., “Analytical Solutions for the Static Analysis of Laminated Composite and Sandwich Plates Based on Higher Order Refined Theory,” Composite Structures, Vol. 56, No. 4, pp. 329� 344 (2002). doi: 10.1016/S0263-8223(02)00017-X
- [18] Kant, T. and Swaminathan, K., “Analytical Solutions for Free Vibration Analysis of Laminated Composite and Sandwich Plates Based on Higher Order Refined Theory,” Composite Structures, Vol. 53, No. 1, pp. 73�85 (2001). doi: 10.1016/S0263-8223(00)00180-X
- [19] Kumar, G. A., Kumar, K. R. and Tarun, K., “Higher Order Closed Form Solutions for Free Vibration of Laminated Composite and Sandwich Shells,” Journal of Sandwich Structures and Materials, Vol. 8, No. 3, pp. 205�235 (2006). doi: 10.1177/1099636206062569
- [20] Golmakani, M. E. and Kadkhodayan, M., “Nonlinear Bending Analysis of Annular FGM Plates Using Higher Order Shear Deformation Plate Theories,” Composite Structures, Vol. 93, pp. 973�982 (2011). doi: 10.1016/ j.compstruct.2010.06.024
- [21] Matsunaga, H., “Free Vibration and Stability of Functionally Graded Plates According to a 2-D HigherOrder Deformation Theory,” Composite Structures, Vol. 82, pp. 499�512 (2008). doi: 10.1016/j.compstruct. 2007.01.030
- [22] Matsunaga, H., “Stress Analysis of Functionally Graded Plates Subjected to Thermal and Mechanical Loadings,” Composite Structures, Vol. 87, pp. 344�357 (2009). doi: 10.1016/j.compstruct.2008.02.002
- [23] Xiang, S. and Kang, G. W., “A Nth-Order Shear Deformation Theory for the Bending Analysis on the Functionally Graded Plates,” European Journal of Mechanics A/Solids, Vol. 37, pp. 336�343 (2013). doi: 10.1016/j.euromechsol.2012.08.005
- [24] Neves, A. M. A., Ferreira, A. J. M., Carrera, E, Cinefra, M., Roque, C. M. C., Jorge, R. M. N. and Soares, C. M. M., “Free Vibration Analysis of Functionally Graded Shells by a Higher-Order Shear Deformation Theory and Radial Basis Functions Collocation, Accounting for Through-the-Thickness Deformations,” European Journal of Mechanics A/Solids, Vol. 37, pp. 24�34 (2013). doi: 10.1016/j.euromechsol. 2012.05.005
- [25] Sahmani, S. and Ansari, R., “On the Free Vibration Response of Functionally Graded Higher-Order Shear Deformable Microplates Based on the Strain Gradient Elasticity Theory,” Composite Structures, Vol. 95, pp. 430�442 (2013). doi: 10.1016/j.compstruct.2012.07.025
- [26] Saidi, A. R., Atashipour, S. R. and Jomehzadeh, E., “Reformulation of Navier Equations for Solving ThreeDimensional Elasticity Problems with Applications to Thick Plate Analysis,” Acta Mech., Vol. 208, pp. 227� 235 (2009). doi: 10.1007/s00707-009-0147-6
- [27] Hasani Baferani, A., Saidi, A. R. and Jomehzadeh, E., “An Exact Solution for Free Vibration of Thin Functionally Graded Rectangular Plates,” Proc. of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, March 1, Vol. 225, No. 3, pp. 526�536 (2011). doi: 10.1243/09544062 JMES2171
- [28] Maziar, J. and Iman, R., “Free Vibration Analysis of Functionally Graded Plates with Multiple Circular and Noncircular Cutouts,” Chinese Journal of Mechanical Engineering, Vol. 24, a, No. 6, a, pp. 1�9 (2011). doi: 10.3901/CJME.2012.02.277
- [29] Batra, R. C. and Jin, J., “Natural Frequencies of a Functionally Graded Anisotropic Rectangular Plate,” Journal of Sound and Vibration, Vol. 282, No. 1�2, pp. 509�516 (2005). doi: 10.1016/j.jsv.2004.03.068
- [30] Ferreira, A. J. M., Batra, R. C., Roque, C. M. C., Qian, L. F. and Jorge, R. M. N., “Natural Frequencies of Functionally Graded Plates by a Meshless Method,” Composite Structures, Vol. 75, No. 1�4, pp. 593�600 (2006). doi: 10.1016/j.compstruct.2006.04.018
- [31] Vel, S. S. and Batra, R. C., “Three-Dimensional Exact Solution for the Vibration of Functionally Graded Rectangular Plates,” Journal of Sound and Vibration, Vol. 272, pp. 703�730 (2004). doi: 10.1016/S0022- 460X(03)00412-7
- [32] Reddy, J. N. and Phan, N. D., “Stability and Vibration of Isotropic and Laminated Plates According to Higher Order Shear Deformation Theory,” Journal of Sound and Vibration, Vol. 98, pp. 157�170 (1985). doi: 10.1016/0022-460X(85)90383-9
- [33] Roque, C. M. C., Ferreira, A. J. M. and Jorge, R. M. N., “ARadial Basis Function Approach for the Free Vibration Analysis of Functionally Graded Plates Using a Refined Theory,” Journal of Sound and Vibration, Vol. 300, No. 3�5, pp. 1048�1070 (2007). doi: 10.1016/ j.jsv.2006.08.037
- [34] Cheng, Z. Q. and Batra, R. C., “Exact Correspondence between Eigenvalues of Membranes and Functionally Graded Simply Supported Polygonal Plates,” Journal of Sound and Vibration, Vol. 229, pp. 879�895 (2000). doi: 10.1006/jsvi.1999.2525
- [35] Mallikarjuna, K. T., “Free Vibration of Symmetrically Laminated Plates Using a Higher Order Theory with Finite Element Technique,” International Journal of Numerical Methods in Engineering, Vol. 28, pp. 1875�1889 (1989). doi: 10.1002/nme.1620280812
- [36] Zhao, X., Lee, Y. Y. and Liew, K. M., “Free Vibration Analysis of Functionally Graded Plates Using the Element-Free kp-Ritz Method,” Journal of Sound and Vibration, Vol. 319, No. 3, pp. 918�939 (2009). doi: 10.1016/j.jsv.2008.06.025
- [37] Hosseini-Hashemi, Sh., Rokni Damavandi Taher, H., Akhavan, H. and Omidi, M., “Free Vibration of Functionally Graded Rectangular Plates Using First-Order Shear Deformation Plate Theory,” Journal of Applied Mathematical Modelling, Vol. 34, No. 5, pp. 1276� 1291 (2010). doi: 10.1016/j.apm.2009.08.008
- [38] Pradyumna, S. and Bandyopadhyay, J. N., “Free Vibration Analysis of Functionally Graded Curved Panels Using a Higher-Order Finite Element Formulation,” Journal of Sound and Vibration, Vol. 318, No. 1�2, pp. 176�192 (2008). doi: 10.1016/j.jsv.2008.03.056
- [39] Fares, M. E., Elmarghany, M. Kh. and Atta, D., “An Efficient and Simple Refined Theory for Bending and Vibration of Functionally Graded Plates,” Composite Structures, Vol. 91, No. 3, pp. 296�305 (2009). doi: 10.1016/j.compstruct.2009.05.008
- [40] Talha, M. and Singh, B. N., “Static Response and Free Vibration Analysis of FGM Plates Using Higher Order Shear Deformation Theory,” Applied Mathematical Modelling, Vol. 34, No. 12, pp. 3991�4011 (2010). doi: 10.1016/j.apm.2010.03.034
- [41] Hassen, A., Abdelouahed, T., Ismail, M. and Adda Bedia, El., “Free Vibration Analysis of Functionally Graded Plates Resting on Winkler-Pasternak Elastic Foundations Using a New Shear Deformation Theory,” International Journal of Mechanics and Materials in Design, Vol. 6, No. 2, pp. 113�121 (2010).
- [42] Hosseini-Hashemi, Sh., Fadaee, M. and Atashipour, S. R., “Study on the Free Vibration of Thick Functionally Graded Rectangular Plates According to a New Exact Closed-Form Procedure,” Composite Structures, Vol. 93, No. 2, pp. 722�735 (2011). doi: 10.1016/j. compstruct.2010.08.007
- [43] Pucha, N. S. and Reddy, J. N., “Stability and Natural Vibration Analysis of Laminated Plates by Using a Mixed Element Based on a Refined Plate Theory,” Journal of Sound and Vibration, Vol. 104, pp. 285� 300 (1986). doi: 10.1016/0022-460X(86)90269-5
- [44] Marur, S. R. and Kant, T., “Free Vibration Analysis of Firbre Reinforced Composite Beams Using Higher Order Theories and Finite Element Modeling,” Journal of Sound and Vibration, Vol. 194, pp. 337�351 (1996). doi: 10.1006/jsvi.1996.0362
- [45] Liu, G. R., Zhao, X., Dai, K. Y., Zhong, Z. H., Li, G. Y. and Han, X., “Static and Free Vibration Analysis of Laminated Composite Plates Using the Conforming Radial Point Interpolation Method,” Composites Science and Technology, Vol. 68, pp. 354�366 (2008). doi: 10.1016/j.compscitech.2007.07.014
- [46] Mirtalaie1, S. H., Hajabasi, M. A. and Hejripour, F., “Free Vibration Analysis of Functionally Graded Moderately Thick Annular Sector Plates Using Differential Quadrature Method,” Applied Mechanics and Materials, Vol. 110�116, pp. 2990�2998 (2012). doi: 10.4028/www.scientific.net/AMM.110-116.2990
- [47] Sina, S. A., Navazi, H. M. and Haddadpour, H., “An Analytical Method for Free Vibration Analysis of Functionally Graded Beams,” Materials and Design, Vol. 30, pp. 741�747 (2009). doi: 10.1016/j.matdes. 2008.05.015
- [48] Fallah, A., Aghdam, M. M. and Kargarnovin, M. H., “Free Vibration Analysis of Moderately Thick Functionally Graded Plates on Elastic Foundation Using the Extended Kantorovich Method,” Applied Mechanics, Vol. 83, No. 2, pp. 177�191 (2013). doi: 10.1007/ s00419-012-0645-1
- [49] Neves, A. M. A., Ferreira, A. J. M., Carrera, E., Cinefra, M., Roque, C. M. C., Jorge, R. M. N. and Soares, C. M. M., “Static, Free Vibration and Buckling Analysis of Isotropic and Sandwich Functionally Graded Plates Using a Quasi-3D Higher-Order Shear Deformation Theory and Meshless Technique,” Composites: Part B, Vol. 44, pp. 657�674 (2013). doi: 10.1016/j.compositesb.2012.01.089
- [50] Neves, A. M. A., Ferreira, A. J. M., Carrera, E., Cinefra, M., Roque, C. M. C. and Jorge, R. M. N, “A Quasi-3D Sinusoidal Shear Deformation Theory for the Static and Free Vibration Analysis of Functionally Graded Plates,” Composites Part B: Engineering, Vol. 43, pp. 711�725 (2012). doi: 10.1016/j.compositesb. 2011.08.009
- [51] Qiana, L. F., Batrab, R. C. and Chena, L. M., “Static and Dynamic Deformations of Thick Functionally Graded Elastic Plates by Using Higher-Order Shear and Normal Deformable Plate Theory and Meshless Local Petrov-Galerkin Method,” Composites: Part B, Vol. 35, pp. 685�697 (2004). doi: 10.1016/j. compositesb.2004.02.004
- [52] Kant, T. and Manjunatha, B. S., “An Unsymmetric FRC Laminate C0 Finite Element Model with 12 Degrees of Freedom Per Node,” Engineering with Computers, Vol. 5, No. 3, pp. 300�308 (1988). doi: 10. 1108/eb023749