Mingtsu Ho This email address is being protected from spambots. You need JavaScript enabled to view it.¹

¹Graduate School of Opto-Mechatronics and Materials, WuFeng University, Chiayi, Taiwan 621, R.O.C.

REFERENCES

1. [1] Baeva, T., Gordienko, S. and Pukhov, A., “Theory of High-Order Harmonic Generation in Relativistic Laser Interaction with Over-Dense Plasma,” Physical Review E, Vol. 74, 046404 (2006). doi: 10.1103/ PhysRevE.74.046404
2. [2] Bulanov, S. V. et al, “Interaction of an Ultrashort, Relativistically Strong Laser Pulse with an Overdense Plasma,” Phys. Plasmas, Vol. 1, pp. 745757 (1994). doi: 10.1063/1.870766
3. [3] Kleinman, R. E. and Mack, R. B., “Scattering by Linearly Vibrating Objects,” IEEE Trans. Antennas Propagation, Vol. AP-27, No. 3, pp. 344352 (1979). doi: 10.1109/TAP.1979.1142085
4. [4] Cooper, J., “Scattering of Electromagnetic Fields by a Moving Boundary: The One-Dimensional Case,” IEEE Trans. Antennas Propagation, Vol. AP-28, No. 6, pp. 791795 (1980). doi: 10.1109/TAP.1980.1142445
5. [5] Harfoush, F., Taflove, A. and Kriegsmann, G., “A Numerical Technique for Analyzing Electromagnetic Wave Scattering from Moving Surfaces in One and Two Dimensions,” IEEE Trans. Antennas Propagation, Vol. 37, No. 1, pp. 5563 (1989). doi: 10.1109/ 8.192164
6. [6] Cooper, J., “Longtime Behavior and Energy Growth for Electromagnetic Waves Reflected by a Moving Boundary,” IEEE Trans. Antennas Propagation, Vol. 41, No. 10, pp. 13651370 (1993). doi: 10.1109/8. 247776
7. [7] Borkar, S. R. and Yang, R. F. H., “Scattering of Electromagnetic Waves from Rough Oscillating Surface Using Spectral Fourier Method,” IEEE Transactions on Antennas and Propagation, Vol. 21, No. 5, pp. 734736 (1973). doi: 10.1109/TAP.1973.1140574
8. [8] Van Bladel, J. and De Zutter, D., “Reflection from Linearly Vibrating Objects: Plane Mirror at Normal Incidence,” IEEE Transactions on Antennas and Propagation, Vol. AP-29, No. 4, pp. 629637 (1981). doi: 10.1109/TAP.1981.1142645
9. [9] De Cupis, P., Gerosa, G. and Schettini, G., “Electromagnetic Scattering by an Object in Relativistic Translational Motion,” Journal of Electromagnetic Waves and Applications (JEMWA), Vol. 14, No. 8, pp. 1037 1062 (2000). doi: 10.1163/156939300X00969
10. [10] De Cupis, P., Burghignoli, P., Gerosa, G. and Marziale, M., “Electromagnetic Wave Scattering by a Perfectly Conducting Wedge in Uniform Translational Motion,” Journal of Electromagnetic Waves and Applications (JEMWA), Vol. 16, No. 8, pp. 345364 (2002). doi: 10.1163/156939302X01182
11. [11] Ciarkowski, A., “Electromagetic Pulse Diffraction by a Moving Half-Plane,” Progress in Electromagnetics Research (PIER), No. 64, pp. 5367 (2006). doi: 10. 2528/PIER06052403
12. [12] Donohoe, J. P., Beggs, J. H. and Ho, M. T., “Comparison of Finite-Difference Time-Domain Results for Scattered Electromagnetic fieLds: Yee Algorithm vs. a Characteristic Based Algorithm,” 27th IEEE Southeastern Symposium on System Theory, pp. 325328 (1995). doi: 10.1109/SSST.1995.390560
13. [13] Ho, M. T., Lai, F. S., Tan, S. W. and Chen, P. W., “Numerical Simulation of Propagation of EM Pulse through Lossless Non-Uniform Dielectric Slab Using Characteristic-Based Method,” Progress in Electromagnetic Research (PIER), No. 81, pp. 197212 (2008). doi: 10.2528/PIER08010303
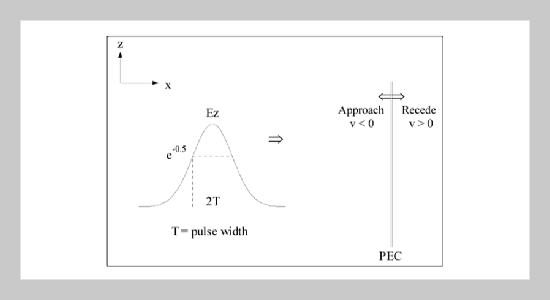
14. [14] Ho, M. T., “One-Dimensional Simulation of Reflected EM Pulses from Objects Vibrating at Different Frequencies,” Progress in Electromagnetics Research (PIER), No. 53, pp. 239248 (2005). doi: 10.2528/ PIER04100502
15. [15] Ho, M. T., “Propagation of Electromagnetic Pulse onto a Moving Lossless Dielectric Half-Space: One-Dimensional Simulation Using Characteristic-Based Method,” Journal of Electromagnetic Waves and Applications (JEMWA), Vol. 19, No. 4, pp. 469478 (2005). doi: 10.1163/1569393053303910