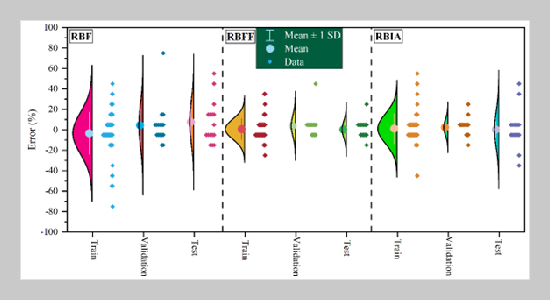
- [1] G.G.Tejani, B. Sadaghat, and S. Kumar, (2023) “Pre dict the maximum dry density of soil based on individual and hybrid methods of machine learning" Advances in engineering and intelligence systems 2(03): 98–109.
- [2] A.Majdi and M.Rezaei, (2013) “Prediction of uncon f ined compressive strength of rock surrounding a road wayusingartificial neural network" Neural Computing and Applications 23: 381–389.
- [3] E. C. Koncagül and P. M. Santi, (1999) “Predicting the unconfined compressive strength of the Breathitt shale using slake durability, Shore hardness and rock structural properties" International Journal of Rock Mechanics and Mining Sciences 36(2): 139–153.
- [4] H. Mendieta. “Determination of a correlation be tween intact rock unconfined compressive strength and index parameters”. In: ISRM Congress. ISRM. 2011, ISRM–12CONGRESS.
- [5] R.Ulusay,Ö.Aydan,Z.A.Erguler,D.J.Ngan-Tillard, T. Seiki, W. Verwaal, Y. Sasaki, and A. Sato, (2015) “ISRM suggested method for the needle penetration test" The ISRMsuggested methods for rock characteri zation, testing and monitoring: 2007-2014: 143–155.
- [6] N.Ceryan, U. Okkan, and A. Kesimal, (2012) “Appli cation of generalized regression neural networks in pre dicting the unconfined compressive strength of carbon ate rocks" Rock mechanics and rock engineering 45: 1055–1072.
- [7] H.AokiandY. Matsukura, (2008) “Estimating the un confined compressive strength of intact rocks from Equotip hardness" Bulletin of Engineering Geology and the Environment 67: 23–29.
- [8] W.Hujer,T.Finkbeiner, and M.Persaud.“Estimating rock strength from non-destructive strength testing (Equotip) and related benefits”. In: EAGE Workshop on Geomechanics in the Oil and Gas Industry. European Association of Geoscientists & Engineers. 2014, cp 397.
- [9] M. Adamu, A. Çolak, I. Umar, Y. Ibrahim, and M. Hamza, (2023) “An Intelligent Approach for Predicting Mechanical Properties of High-Volume Fly Ash (HVFA) Concrete" Civil Engineering Journal (Iran) 9(9):
- [10] R. Balamuralikrishnan, A. Al-Mawaali, M. Al Yaarubi, B. Al-Mukhaini, and A. Kaleem, (2023) “Seis mic upgradation of RC beams strengthened with exter nally bonded spent catalyst based ferrocement laminates" HighTech and Innovation Journal 4(1): 189–209.
- [11] M.Sudhir and M.Beulah, (2023) “Multigene Genetic Programming Based Prediction of Concrete Fracture Pa rameters of Unnotched Specimens" Civil Engineering Journal 9(2): 393–410.
- [12] S. Dehghan, G. Sattari, S. C. Chelgani, and M. Aliabadi, (2010) “Prediction of uniaxial compressive strength and modulus of elasticity for Travertine samples using regression and artificial neural networks" Mining Science and Technology (China) 20(1): 41–46.
- [13] F. Meulenkamp and M. A. Grima, (1999) “Application of neural networks for the prediction of the unconfined compressive strength (UCS) from Equotip hardness" In ternational Journal of rock mechanics and mining sciences 36(1): 29–39.
- [14] D. Mishra and A. Basu, (2013) “Estimation of uniax ial compressive strength of rock materials by index tests using regression analysis and fuzzy inference system" Engineering Geology 160: 54–68.
- [15] H. Sonmez, E. Tuncay, and C. Gokceoglu, (2004) “Models to predict the uniaxial compressive strength and the modulus of elasticity for Ankara Agglomerate" Inter national Journal of Rock Mechanics and Mining Sciences 41(5): 717–729.
- [16] C. Gokceoglu and K. Zorlu, (2004) “A fuzzy model to predict the uniaxial compressive strength and the modulus of elasticity of a problematic rock" Engineering Appli cations of Artificial Intelligence 17(1): 61–72.
- [17] J. Sun, J. Zhang, Y. Gu, Y. Huang, Y. Sun, and G. Ma, (2019) “Prediction of permeability and unconfined compressive strength of pervious concrete using evolved support vector regression" Construction and Building Materials 207: 440–449.
- [18] X. Lu, W. Zhou, X. Ding, X. Shi, B. Luan, and M. Li, (2019) “Ensemble learning regression for estimating un confined compressive strength of cemented paste backfill" IEEE access 7: 72125–72133.
- [19] N.Yesiloglu-Gultekin, C. Gokceoglu, and E. A. Sezer, (2013) “Prediction of uniaxial compressive strength of granitic rocks by various nonlinear tools and comparison of their performances" International Journal of Rock Mechanics and Mining Sciences 62: 113–122.
- [20] A.Cevik,E.A.Sezer,A.F.Cabalar,andC.Gokceoglu, (2011) “Modeling of the uniaxial compressive strength of some clay-bearing rocks using neural network" Applied Soft Computing 11(2): 2587–2594.
- [21] M.Rezaei and M. Asadizadeh, (2020) “Predicting un confined compressive strength of intact rock using new hybrid intelligent models" Journal of Mining and En vironment 11(1): 231–246.
- [22] V. Singh, D. Singh, and T. Singh, (2001) “Prediction of strength properties of some schistose rocks from petro graphic properties using artificial neural networks" In ternational Journal of Rock Mechanics and Mining Sciences 38(2): 269–284.
- [23] A. Alavi, A. Gandomi, M. Gandomi, and S. Sadat Hosseini, (2009) “Prediction of maximum dry density and optimum moisture content of stabilised soil using RBF neural networks" The IES Journal Part A: Civil &Structural Engineering 2(2): 98–106.
- [24] M. R. Sabour and S. M. A. Movahed, (2017) “Appli cation of radial basis function neural network to predict soil sorption partition coefficient using topological descrip tors" Chemosphere 168: 877–884.
- [25] R. A. A. Heshmati, A. H. Alavi, M. Keramati, and A. H. Gandomi. “A radial basis function neural net work approach for compressive strength prediction of stabilized soil”. In: Road pavement material character ization and rehabilitation: selected papers from the 2009 geohunan international conference. 2009, 147–153.
- [26] M. K. Habib and A. K. Cherri, (1998) “Parallel qua ternary signed-digit arithmetic operations: addition, sub traction, multiplication and division" Optics & Laser Technology 30(8): 515–525.
- [27] L. Abualigah, A. Diabat, S. Mirjalili, M. Abd Elaziz, and A. H. Gandomi, (2021) “The arithmetic optimiza tion algorithm" Computer methods in applied me chanics and engineering 376: 113609.
- [28] Y.-P. Xu, J.-W. Tan, D.-J. Zhu, P. Ouyang, and B. Taheri, (2021) “Model identification of the proton ex change membrane fuel cells by extreme learning machine and a developed version of arithmetic optimization algo rithm" Energy Reports 7: 2332–2342.
- [29] L. Abualigah, A. Diabat, P. Sumari, and A. H. Gan domi, (2021) “A novel evolutionary arithmetic optimiza tion algorithm for multilevel thresholding segmentation of covid-19 ct images" Processes 9(7): 1155.
- [30] A.KavehandK.B.Hamedani.“Improvedarithmetic optimization algorithm and its application to discrete structural optimization”. In: Structures. 35. Elsevier. 2022, 748–764.
- [31] K. Zervoudakis and S. Tsafarakis, (2023) “A global optimizer inspired from the survival strategies of flying foxes" Engineering with Computers: 1–34.
- [32] Z. Liu, P. Jiang, J. Wang, and L. Zhang, (2021) “En semble forecasting system for short-term wind speed fore casting based on optimal sub-model selection and multi objective version of mayfly optimization algorithm" Ex pert Systems with Applications 177: 114974.
- [33] S. Kumar, G. G. Tejani, and S. Mirjalili, (2019) “Modi f ied symbiotic organisms search for structural optimiza tion" Engineering with Computers 35(4): 1269–1296.
- [34] S. Kumar, G. G. Tejani, N. Pholdee, and S. Bureerat, (2021) “Multi-objective passing vehicle search algorithm for structure optimization" Expert Systems with Ap plications 169: 114511.
- [35] R. L. Haupt. Practical genetic algorithms. 2004. [36] S. Tsafarakis, K. Zervoudakis, A. Andronikidis, and E. Altsitsiadis, (2020) “Fuzzy self-tuning differential evolution for optimal product line design" European Journal of Operational Research 287(3): 1161–1169.
- [37] M.S. Nobile, P. Cazzaniga, D. Besozzi, R. Colombo, G. Mauri, and G. Pasi, (2018) “Fuzzy Self-Tuning PSO: Asettings-free algorithm for global optimization" Swarm and evolutionary computation 39: 70–85.
- [38] E. T. Mohamad, D. Jahed Armaghani, E. Momeni, and S. V. Alavi Nezhad Khalil Abad, (2015) “Predic tion of the unconfined compressive strength of soft rocks: a PSO-based ANN approach" Bulletin of Engineering Geology and the Environment 74: 745–757.
- [39] M. Rezaei, A. Majdi, and M. Monjezi, (2014) “An intelligent approach to predict unconfined compressive strength of rock surrounding access tunnels in longwall coal mining" Neural Computing and Applications 24: 233–241.
- [40] A. Majdi and M. Rezaei, (2013) “Prediction of uncon f ined compressive strength of rock surrounding a road wayusingartificial neural network" Neural Computing and Applications 23: 381–389.
- [41] N. Ceryan, U. Okkan, and A. Kesimal, (2013) “Pre diction of unconfined compressive strength of carbonate rocks using artificial neural networks" Environmental earth sciences 68: 807–819.
- [42] B.Narendra,P.Sivapullaiah, S. Suresh, and S. Omkar, (2006) “Prediction of unconfined compressive strength of soft grounds using computational intelligence techniques: A comparative study" Computers and Geotechnics 33(3): 196–208.